Privacy Preserving Morphological Operations for Digital Images

Image processing operations require complex computations. The emerging cloud technologies provide businesses and individuals with the possibility to outsource these computations on a remote platform with large resources and high availability. This approach substantially reduces the costs, but raises privacy concerns. To address these concerns, the data (i.e. the images) owned by the user could be encrypted, sent to the cloud and processed there by taking advantage from the properties of a homomorphic encryption scheme. The result of the computation performed on encrypted data is sent back to the user to be decrypted.

In the paper the authors study the possibility of performing some morphological operations on encrypted digital images. The chosen operations, when represented as plaintext operations in the field $\mathbb {F} _{2}$ are modelled by very sparse polynomials of large degree. This makes them very suitable to be performed homomorphically using the certSGN scheme.

The authors of the paper have implemented these operations using the certSGN, the BGV and the BFV schemes. The results are discussed and compared.

Morphological primitives

Morphology refers to the description of the properties concerning the shape and structure of an object. In the context of image processing, this is related to the description of properties of shapes of areas in an image.

So-called morphology operators are used to extract properties of the image, useful for its descriptions (such as the contour, skeletons or convex hulls). One has to input two parameters: a binary image and a structural element which describes some geometrical shape and is much smaller than the processed image.

Binary images

The pixels in a binary image are partitioned in two disjoint sets: objects and background. Morphological operations between a chosen structural element and the image can be expressed as classical set-theoretic operations (such as intersections and unions).

A black and white image can be represented as a binary matrix, where value $0$ represents the background pixels and value $1$ represents pixels that are associated to objects.

Structring elements

A structural (or structuring) element consists of a description of a certain shape, typically much smaller than the processed image. The most common elements have a special nume: box (rectangle of a given size), disk or ring.

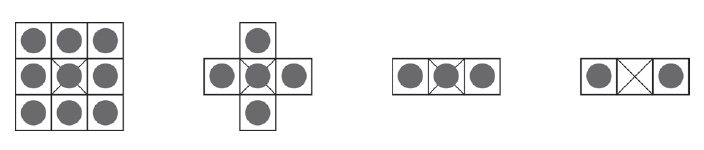
Elements of a structuring element $S$ can be viewed as pairs of integers which are measured with respect to the ``origin" $(0,0)$ of the element, a pixel which is usually crossed in diagram representations.

Generally, the origin of the structuring element is chosen to be the pixel located at the center.

An operation commonly used to compute the result of a certain morphological primitive is the translation. If $p\in \mathbb {Z} ^{2}$ is a fixed vector, then the translation of $S$ by $p$ is $S_{p}=\{s+p\mid s\in S\}$, where $+$ represents the vector addition in $\mathbb {Z} ^{2}$.

The erosion operation

We see images $I$ and structural elements $S$ as finite subsets of $\mathbb {Z} ^{2}$.

The erosion $E(I,S)$ is the set of pixels $p$ for which the translated structural element $S_{p}$ is contained in the image $I$. That is,

$E(I,S)=I\ominus S=\{p\in I\mid S_{p}\subseteq I\}$.

Intuitively, after an erosion operation is performed, the set $E(I,S)$ retains only the positions in the image for which all pixels of the translated structural element belong to the object set.

Below we see an example of erosion operation.

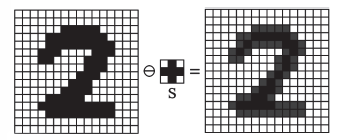
Images $I$ can be represented by binary matrices $A$, where we represent $1$ as an object in the image and $0$ as background. To compute the eroded image $I'$, represented by a matrix $A'$ one must check whether for all elements $p\in I$, the equality $A[x][y]=1$ holds for all pixels $s=(x,y)\in S_{p}$.

If it holds, then the pixel $p\in I$ is kept in the image $I'$ and the corresponding element from the matrix $A'$ is set to be equal $1$.

One can see that for each $p=(i,j)\in I$, the entry $(i,j)$ in the eroded matrix $A'$ can be computed as

$A'[i][j]=\prod \limits _{s\in S_{p}}A[s_{x}][s_{y}].$

This computation can be done in an encrypted manner if the encryption scheme is homomorphic with respect to multiplication, like the certSGN scheme.

The dilation operation

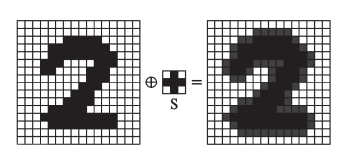
The dilation of $I$ with the structural element $S$ is defined as $D(I,S)=I\oplus S=\{p=(x,y)\in \mathbb {Z} ^{2}\mid S_{p}\cap I\neq \emptyset \}.$

That is, the dilation retains all the pixels $p$ for which the translated structured element $S_{p}$ intersects non-trivially with the image. Below we see the effects of a dilation with a structured element $S$.