Difference between revisions of "Privacy Preserving Morphological Operations for Digital Images"
| (24 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
The chosen operations, when represented as plaintext operations in the field <math>\mathbb F_2</math> are modelled by very sparse polynomials of large degree. This makes them very suitable to be performed homomorphically using the [[certSGN]] scheme. | The chosen operations, when represented as plaintext operations in the field <math>\mathbb F_2</math> are modelled by very sparse polynomials of large degree. This makes them very suitable to be performed homomorphically using the [[certSGN]] scheme. | ||
| − | The authors of the paper have implemented these operations using the [certSGN], the [[BGV]] and the [[BFV]] schemes. The results are discussed and compared. | + | The authors of the paper have implemented these operations using the [[certSGN]], the [[BGV]] and the [[BFV]] schemes. The results are discussed and compared. |
== Morphological primitives == | == Morphological primitives == | ||
| Line 11: | Line 11: | ||
So-called morphology operators are used to extract properties of the image, useful for its descriptions (such as the contour, skeletons or convex hulls). One has to input two parameters: a binary image and a structural element which describes some geometrical shape and is much smaller than the processed image. | So-called morphology operators are used to extract properties of the image, useful for its descriptions (such as the contour, skeletons or convex hulls). One has to input two parameters: a binary image and a structural element which describes some geometrical shape and is much smaller than the processed image. | ||
| + | |||
| + | |||
| + | === Binary images === | ||
| + | |||
| + | The pixels in a binary image are partitioned in two disjoint sets: objects and background. Morphological operations between a chosen structural element and the image can be expressed as classical set-theoretic operations (such as intersections and unions). | ||
| + | |||
| + | |||
| + | A black and white image can be represented as a binary matrix, where value <math>0 </math> represents the background pixels and value <math>1 </math> represents pixels that are associated to objects. | ||
| + | |||
| + | === Structring elements === | ||
| + | |||
| + | A structural (or structuring) element consists of a description of a certain shape, typically much smaller than the processed image. The most common elements have a special nume: box (rectangle of a given size), disk or ring. | ||
| + | |||
| + | <center>[[File:Structelements.png]] </center> | ||
| + | |||
| + | Elements of a structuring element <math>S </math> can be viewed as pairs of integers which are measured with respect to the ``origin" <math>(0,0) </math> of the element, a pixel which is usually crossed in diagram representations. | ||
| + | |||
| + | Generally, the origin of the structuring element is chosen to be the pixel located at the center. | ||
| + | |||
| + | An operation commonly used to compute the result of a certain morphological primitive is the translation. If <math> p \in \mathbb Z^2 </math> is a fixed vector, then the translation of <math> S</math> by <math> p</math> is <math>S_p = \{ s+ p \mid s \in S \} </math>, where <math>+</math> represents the vector addition in <math>\mathbb Z^2 </math>. | ||
| + | |||
| + | === The erosion operation === | ||
| + | |||
| + | We see images <math> I </math> and structural elements <math>S</math> as finite subsets of <math> \mathbb Z^2</math>. | ||
| + | |||
| + | The erosion <math> E(I,S) </math> is the set of pixels <math>p </math> for which the translated structural element <math> S_p </math> is contained in the image <math> I </math>. That is, | ||
| + | |||
| + | <center> <math> E(I,S) = I \ominus S = \{p \in I \mid S_p \subseteq I \} </math>.</center> | ||
| + | |||
| + | Intuitively, after an erosion operation is performed, the set <math> E(I,S) </math> retains only the positions in the image for which all pixels of the translated structural element belong to the object set. | ||
| + | |||
| + | Below we see an example of erosion operation. | ||
| + | |||
| + | <center> [[File:Erosion.png]] </center> | ||
| + | |||
| + | Images <math> I </math> can be represented by binary matrices <math> A </math>, where we represent <math> 1 </math> as an object in the image and <math> 0 </math> as background. To compute the eroded image <math> I'</math>, represented by a matrix <math>A' </math> one must check whether for all elements <math> p \in I </math>, the equality <math>A[x][y]=1 </math> holds for all pixels <math> s=(x,y) \in S_p </math>. | ||
| + | |||
| + | If it holds, then the pixel <math>p \in I </math> is kept in the image <math>I' </math> and the corresponding element from the matrix <math> A'</math> is set to be equal <math> 1 </math>. | ||
| + | |||
| + | One can see that for each <math>p=(i,j) \in I </math>, the entry <math>(i,j)</math> in the eroded matrix <math> A'</math> can be computed as | ||
| + | <center><math>A'[i][j] = \prod\limits_{s \in S_p} A[s_x][s_y].</math></center> | ||
| + | |||
| + | This computation can be done in an encrypted manner if the encryption scheme is homomorphic with respect to multiplication, like the [[certSGN]] scheme. | ||
| + | |||
| + | === The dilation operation === | ||
| + | |||
| + | The dilation of <math> I</math> with the structural element <math> S </math> is defined as | ||
| + | <math>D(I,S) = I \oplus S = \{p=(x,y) \in \mathbb Z^2 \mid S_p \cap I \neq \emptyset \}.</math> | ||
| + | |||
| + | That is, the dilation retains all the pixels <math> p </math> for which the translated structured element <math> S_p </math> intersects non-trivially with the image. Below we see the effects of a dilation with a structured element <math>S</math>. | ||
| + | |||
| + | <center>[[File:Dilation.png]] </center> | ||
| + | |||
| + | Using the notations in the previous subsection, the entries of a binary matrix associated to a dilated image can be computed from the following equality. | ||
| + | |||
| + | <center><math> 1-A'[i][j] = \prod_{s \in S_p} (1- A[s_x][s_y]).</math></center> | ||
| + | |||
| + | This expression can be simplified if one represents binary images as matrices whose <math> 0 </math> entries represent objects and <math> 1 </math> represents background. | ||
| + | |||
| + | === Other morphological operations === | ||
| + | |||
| + | Using the primitives described above one can perform edge dection, as the <math> \mathbb F_2 </math> difference between the initial image and its eroded version. This is described in the image below. | ||
| + | <center> [[File:Edgedetection.png]] </center> | ||
| + | |||
| + | <b> Opening </b> and <b> closing </b> are other morphological operations. | ||
| + | |||
| + | The opening of <math>I</math> with <math> S </math> is performed in the following way: | ||
| + | |||
| + | 1. <math>I_0 </math> is the erosion of <math> I </math> by <math>S</math>. | ||
| + | |||
| + | 2. Let <math> S' = \{-s \mid s \in S \} </math> the symmetric of <math> S</math> with respect to the origin (its center). | ||
| + | |||
| + | 3. The opening <math>I' </math> is the dilation of <math> I_0 </math> with the structural element <math> S' </math>. | ||
| + | |||
| + | The erosion carried out first eliminates the noise and shrinks the object shape, while the next dilation expands the object back, but without the eliminated noise. | ||
| + | |||
| + | A similar operation, the closing of <math> I </math> with <math> S </math> is performed as: | ||
| + | |||
| + | 1. <math> I_0 </math> is the dilation of <math> I </math> by <math> S</math>. | ||
| + | |||
| + | 2. <math> S' </math> is the symmetric of <math> S </math> defined above. | ||
| + | |||
| + | 3. The closing <math> I </math> is the erosion of <math> I_0 </math> with the structural element <math> S' </math>. | ||
| + | |||
| + | |||
| + | <center> [[File:Openingclosing.png]] </center> | ||
| + | |||
| + | == Experiments and conclusions == | ||
| + | |||
| + | The authors used an implementation of the [[certSGN]] encryption scheme to compute morphological primitives over an encrypted image, and also compared their results with other LWE based schemes such as BGV (HElib) and BFV (Microsoft SEAL). | ||
| + | |||
| + | The experiments show that for certian structural elements the [[certSGN]] implementation presents optimizations of 300x up to 10000x in execution times of morphological primitives and in 2.87x to 55x in memory optimization over the LWE schemes. The details of the experiments can be found in the paper. | ||
== References == | == References == | ||
Latest revision as of 13:07, 7 March 2021
Image processing operations require complex computations. The emerging cloud technologies provide businesses and individuals with the possibility to outsource these computations on a remote platform with large resources and high availability. This approach substantially reduces the costs, but raises privacy concerns. To address these concerns, the data (i.e. the images) owned by the user could be encrypted, sent to the cloud and processed there by taking advantage from the properties of a homomorphic encryption scheme. The result of the computation performed on encrypted data is sent back to the user to be decrypted.
In the paper [1] the authors study the possibility of performing some morphological operations on encrypted digital images. The chosen operations, when represented as plaintext operations in the field are modelled by very sparse polynomials of large degree. This makes them very suitable to be performed homomorphically using the certSGN scheme.
The authors of the paper have implemented these operations using the certSGN, the BGV and the BFV schemes. The results are discussed and compared.
Contents
Morphological primitives
Morphology refers to the description of the properties concerning the shape and structure of an object. In the context of image processing, this is related to the description of properties of shapes of areas in an image.
So-called morphology operators are used to extract properties of the image, useful for its descriptions (such as the contour, skeletons or convex hulls). One has to input two parameters: a binary image and a structural element which describes some geometrical shape and is much smaller than the processed image.
Binary images
The pixels in a binary image are partitioned in two disjoint sets: objects and background. Morphological operations between a chosen structural element and the image can be expressed as classical set-theoretic operations (such as intersections and unions).
A black and white image can be represented as a binary matrix, where value represents the background pixels and value represents pixels that are associated to objects.
Structring elements
A structural (or structuring) element consists of a description of a certain shape, typically much smaller than the processed image. The most common elements have a special nume: box (rectangle of a given size), disk or ring.
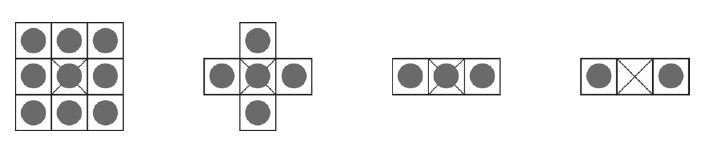
Elements of a structuring element can be viewed as pairs of integers which are measured with respect to the ``origin" of the element, a pixel which is usually crossed in diagram representations.
Generally, the origin of the structuring element is chosen to be the pixel located at the center.
An operation commonly used to compute the result of a certain morphological primitive is the translation. If is a fixed vector, then the translation of by is , where represents the vector addition in .
The erosion operation
We see images and structural elements as finite subsets of .
The erosion is the set of pixels for which the translated structural element is contained in the image . That is,
Intuitively, after an erosion operation is performed, the set retains only the positions in the image for which all pixels of the translated structural element belong to the object set.
Below we see an example of erosion operation.
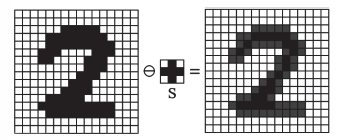
Images can be represented by binary matrices , where we represent as an object in the image and as background. To compute the eroded image , represented by a matrix one must check whether for all elements , the equality holds for all pixels .
If it holds, then the pixel is kept in the image and the corresponding element from the matrix is set to be equal .
One can see that for each , the entry in the eroded matrix can be computed as
This computation can be done in an encrypted manner if the encryption scheme is homomorphic with respect to multiplication, like the certSGN scheme.
The dilation operation
The dilation of with the structural element is defined as
That is, the dilation retains all the pixels for which the translated structured element intersects non-trivially with the image. Below we see the effects of a dilation with a structured element .
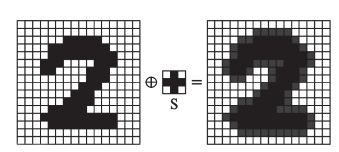
Using the notations in the previous subsection, the entries of a binary matrix associated to a dilated image can be computed from the following equality.
This expression can be simplified if one represents binary images as matrices whose entries represent objects and represents background.
Other morphological operations
Using the primitives described above one can perform edge dection, as the difference between the initial image and its eroded version. This is described in the image below.

Opening and closing are other morphological operations.
The opening of with is performed in the following way:
1. is the erosion of by .
2. Let the symmetric of with respect to the origin (its center).
3. The opening is the dilation of with the structural element .
The erosion carried out first eliminates the noise and shrinks the object shape, while the next dilation expands the object back, but without the eliminated noise.
A similar operation, the closing of with is performed as:
1. is the dilation of by .
2. is the symmetric of defined above.
3. The closing is the erosion of with the structural element .

Experiments and conclusions
The authors used an implementation of the certSGN encryption scheme to compute morphological primitives over an encrypted image, and also compared their results with other LWE based schemes such as BGV (HElib) and BFV (Microsoft SEAL).
The experiments show that for certian structural elements the certSGN implementation presents optimizations of 300x up to 10000x in execution times of morphological primitives and in 2.87x to 55x in memory optimization over the LWE schemes. The details of the experiments can be found in the paper.
References
- ↑ C. Lupascu, C. Plesca, M. Togan, Privacy Preserving Morphological Operations for Digital Images, 2020 13th International Conference on Communications (COMM), Bucharest, Romania, 2020, pp. 183-188, doi: 10.1109/COMM48946.2020.9141997.


















![{\displaystyle A[x][y]=1 }](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/7edebd38768052b53e1d6979ae617d5389659541)



![{\displaystyle A'[i][j] = \prod\limits_{s \in S_p} A[s_x][s_y].}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/05cd8090f706cf657487314e90d8266d0dabecd2)

![{\displaystyle 1-A'[i][j] = \prod_{s \in S_p} (1- A[s_x][s_y]).}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/13c81f0e7a04913b19c6e9854abbd863c6738d46)


